2. Løsningsmetode.

Metoden til at finde alle løsninger fandt jeg ved at bearbejde et oplæg i et skrift, hvis forfatter, titel og bladnavn forlængst er glemte. Såvidt jeg husker, skulle et flowdiagram illustrere hop mellem forskellige sætninger, og det var måske Peter Naur eller en anden af datidens koryfæer, der stod bag?

Fremgangsmåden er denne: repræsenter terning og brikker i nogle variable, og begynd så i den ene side af løsningstræet.

2.1 En terning i een dimension.

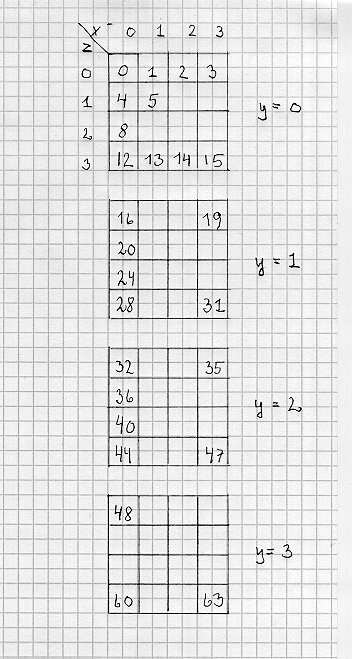
Soma-kuben fylder 3x3x3 felter = 27 felter. Men for at kunne finde "kanterne", må der lægges et lag udenpå de tre af siderne. Derved bliver der 4x4x4 = 64 felter. Det vil sige, at i et xyz-system går terningen fra (0,0,0) til 3,3,3). Men - ikke mindst, fordi programmet blev skrevet til meget små maskiner - det er (var) mere effektivt at bruge et array med dimensionen [0..63]. Omsætningen (x,y,z) til det enstrengede array er jo x+16*y+4*z, mens det den modsatte vej er (plads mod 4,plads div 16,(plads mod 16) div 4). Jeg kalder min array for Braet, og den fyldes med 0 og 1 således fra begyndelsen: (0,0,0,1,0,0,0,1,0,0,0,1, 1,1,1,1, 0,0,0,1, 0,0,0,1, 0,0,0,1, 1,1,1,1, 0,0,0,1, 0,0,0,1, 0,0,0,1, 1,1,1,1, 1,1,1,1, 1,1,1,1, 1,1,1,1, 1,1,1,1); 0 betyder en ledig plads, 1 betyder optaget.